動的計画法マスターへの道(1日目)~パターン数を求めよう~

今回は、パターン数を求めるアルゴリズムについて学習しました。以下は動的計画法をマスターしようと思った背景を書いているだけであるため、気になる方以外は読み飛ばしていただいて問題ないです！

動的計画法をマスターしたいと思った背景。

普段はWebアプリケーションを開発している筆者(大学生)ですが、最近就活を意識し始めました。Webアプリケーション開発を普段からしているからある程度の技術力はあるはず！そう過信していました。

ある日のこと、夏季インターンシップへ参加しようととある企業へ申し込みました。数日後、コーディング試験があるから期日までにやっといてというメールがその企業から送られてきました。まあ、解けるんじゃね、という安易な気持ちの元、特に勉強することなく受験してみたら結果は惨敗。テストケースが２０個くらいあったが、そのうちの半分くらいしかテストを通すことができませんでした。

この出来事から数日間はマジで凹みました。こんな思いはしたくない！そう思い、しっかりとコーディング試験を突破できるくらいの実力をつけるためにアルゴリズムの学習をすることにしました。

本来はAtcoderやLeetCodeで勉強する予定だったのですが、学習していく中で、自分は動的計画法に関してめっぽう弱いということに気がつきました。

動的計画法を用いる場合でも、しっかりとコードが書けるようになりたい。そのために、自分の考えたことや正しい解法を記事にして、知識の整理をしようと思い執筆し始めました。

今回は、その１日目ということでLeetCodeのDynamic ProgrammingにあるEasy問題を解きました。（ここまで読んでいただいた方はありがとうございます）

問題
解法
まとめ

問題

Problem70 Climbing Stairs in Dynamic Programming

問題のリンクはここから

解法

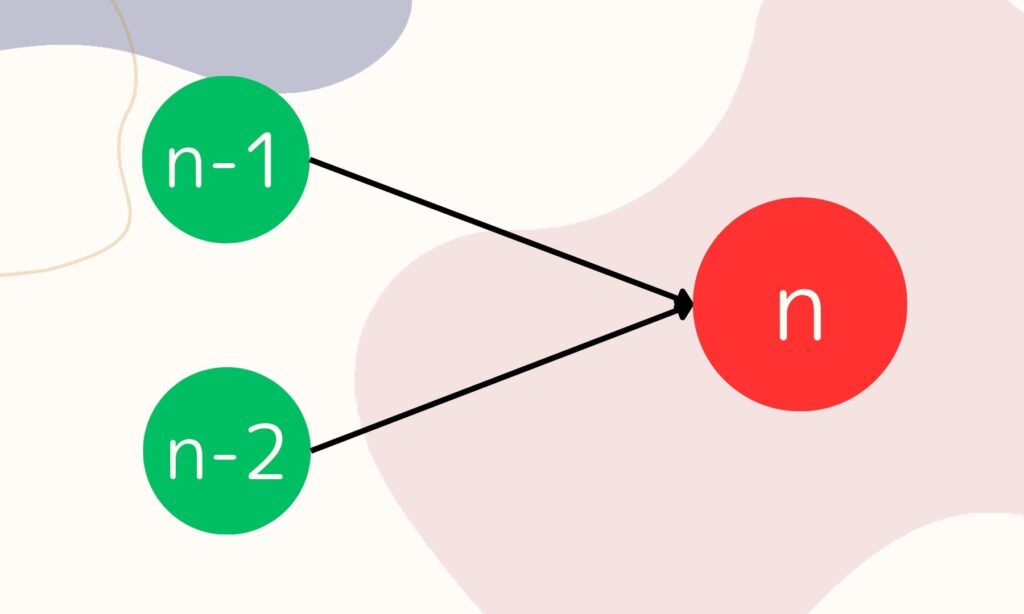
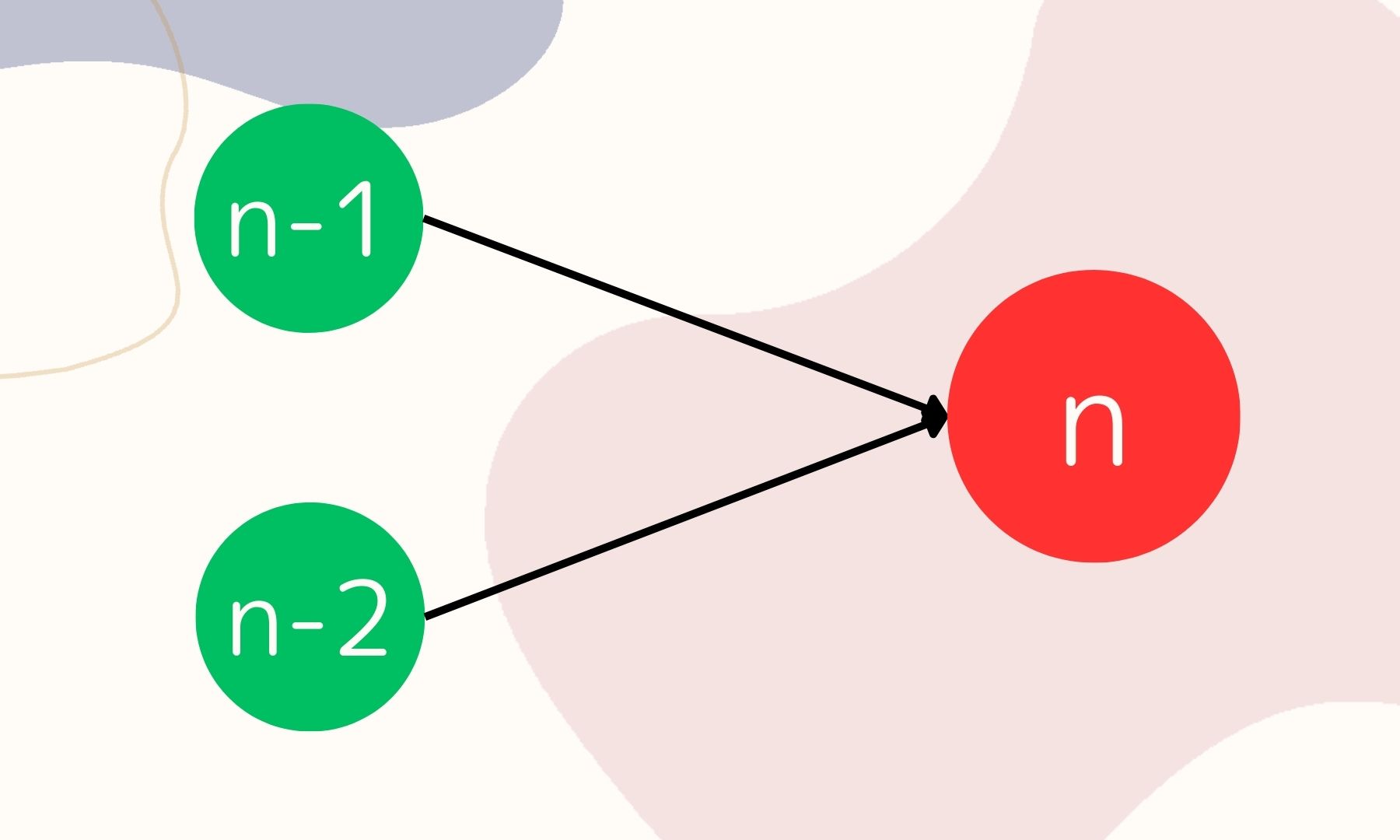
階段のn段目にたどり着くには、

n – 1段目から1段上にあがる
n – 2段目から2段上にあがる

の2パターンしかありません。

よって、n段目(n > 1)までの上り方のパターン数の合計をstep[n]とすると、以下の式が成り立ちます。

step[n] = step[n - 1] + step[n - 2]

よって、n = 2から求めたい段数まで繰り返し計算していくことで答えがでます。

Acceptedされたプログラムは以下の通りです。

def climbStairs(self, n: int) -> int:
        step = [0]*(n+1)
        step[0] = 1; step[1] = 1
        for i in range(2, n+1):
            step[i] = step[i - 1] + step[i - 2]
        return step[n]