グラフ理論は、ネットワークやシステムの構造を理解するための重要な数学分野です。
特に「マッチング」は、就職活動や配車サービスなど、私たちの生活にも深く関わっています。
本記事では、初心者の方にも理解しやすいよう、グラフ理論の基本からマッチング、アルゴリズム、応用までを丁寧に解説します。
「グラフ理論とは?」、「マッチングとは何か?」、「どのように使われるのか?」という疑問にお答えする内容となっていますので、ぜひ最後までお読みください!
- グラフ理論
- マッチング
グラフ理論の用語を確認

まず、グラフ理論の基礎を簡単に復習しましょう!
頂点集合V、辺集合EからなるグラフGを\(G=(V, E)\)と書く
グラフとは、頂点と辺からなるデータ構造のことをいいます。また、\(G=(V, E)\)は頂点集合Vと辺集合EからなるグラフGであるとします。頂点はVertex、辺はEdgeなので、その頭文字をとって頂点集合V、辺集合Eとしています。
次に無向グラフと有向グラフについても確認しましょう。
辺の向きを持たないグラフを無向グラフ、辺の向きを持つグラフを有向グラフと呼びます。
特に、無向グラフの辺を無向辺、有向グラフの辺を有向辺といいます。
頂点uからvへと繋がっている無向辺をuvと書きます。無向辺であるため、vuとしても同じ意味です。一方、頂点uからvへと繋がっている有向辺をuvと表し、頂点uを始点、頂点vを終点と呼びます。有効辺であることから、辺uvと辺vuは別の意味になってしまいます。
辺uvがグラフにあるとき、頂点uとvは隣接しているといい、辺uvは頂点uとvに接続しているといいます。頂点同士が繋がっている(連結している)ときは隣接、辺と頂点がくっついているときは接続と覚えておきましょう。
マッチングとは何か?
マッチングの定義
辺集合Eの部分集合Mについて、Mに含まれる複数の辺は同じ頂点に接続しないとき、Mをマッチングと呼ぶ。
マッチングとは同じ頂点に2辺以上が接続しない辺集合のことです。
サッカーのトーナメントを考えるとわかりやすいです。
1試合をするためには、自チームと相手チームのペアが必要です。これは、1対1の対応であり、1対多になってはいけません。
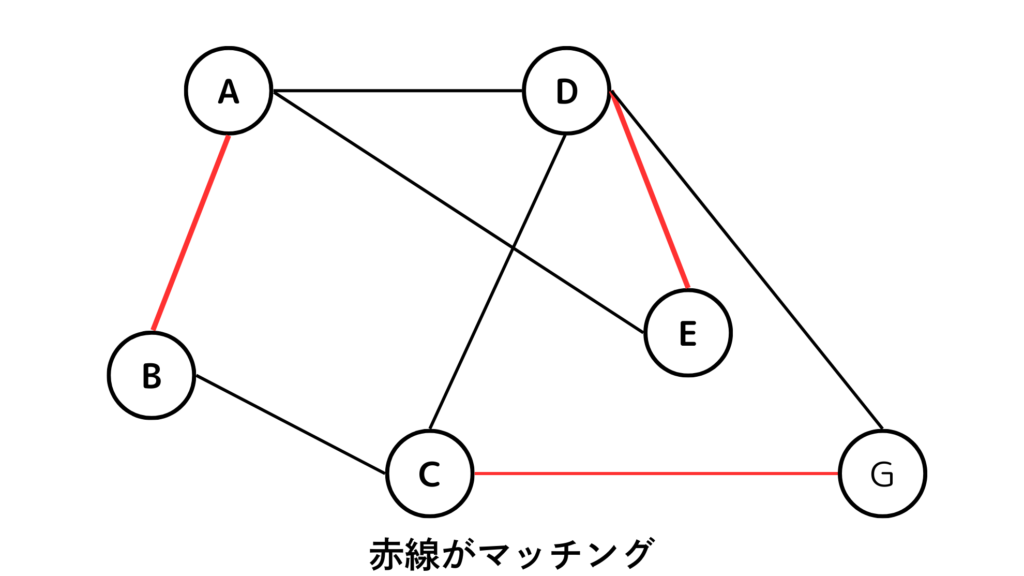
このペアの組み合わせがマッチングに該当します。複数の辺が同じ頂点に接続しないということは、ある頂点に対して隣接している頂点はただ1つに決まります。
ChatGPTにマッチングの例を聞いたら、
- 学校の入学手続き: 生徒と学校の組み合わせ。
- 配車サービス: 利用者とドライバーの最適なマッチング。
をあげてくれました。
最大マッチング
最大マッチング
マッチング\(M\subset{G}\)の中で辺数最大のもの
最大マッチングとは、グラフGのマッチングの中で辺数が最も大きいマッチングのことです。
つまり、いっぱいペアを作れるようにグラフから辺を選択してできた辺集合です。
最大マッチングを求めるアルゴリズムを理解するためには、増加パス(augmenting path)を知っておく必要があります。
増加パス
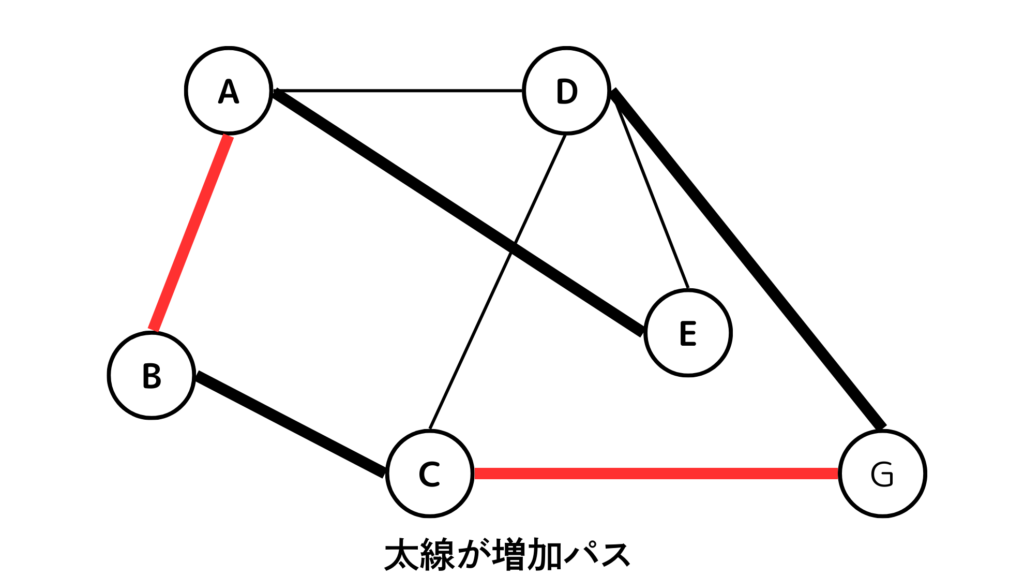
増加パス
- \(v_{1}\ne v_{k}\)かつ\(v_{1}, v_{k}\)はマッチングMによってマッチングされていない
- \(i\)が奇数のとき、\(v_{i}v_{i+1}\notin M, i\)が偶数のとき\(v_{i}v_{i+1}\in M\)である
増加パスはマッチングしている辺としていない辺を交互に通るパスのことです。
ここで注目すべき性質が、増加パスの辺を入れ替える、すなわちマッチングの辺はマッチングから外す、マッチングでない辺はマッチングの辺にする操作を行ったマッチング\(M’\)もマッチングとなっている点です。(マッチングが多くてすみません。)
\(|S|\)を集合Sの要素数とすると、マッチングM, M’について\(|M’|=|M|+1\)が成立する。
また、増加パスと最大マッチングについて以下の定理が成り立ちます。
定理
マッチングMの増加パスが存在しないことは、Mが最大マッチングであることの必要十分条件である.
(最大マッチングが見つかった)=(増加パスがない)ということになります。
最大マッチングを見つけるアルゴリズム
最大マッチングを見つけるアルゴリズムについて解説します。
- while (Mの増加パスが存在する)
- 増加パスAを元にMを更新する
- Mを出力(Mは最大マッチング)
前章の定理から、Mの増加パスがなくなるまで反復処理を行います。
まとめ

グラフ理論におけるマッチングは、数学的な興味だけでなく、現実社会での課題解決にも大いに役立つ分野です。
本記事では、マッチングの基礎から最大マッチングを見つけるアルゴリズムまでを解説しました。
この記事をきっかけに、さらに深くグラフ理論について学んでみてはいかがでしょうか。
最後までご覧いただき、ありがとうございます。お疲れ様でした。



コメント