あなたはコンピュータがどのように負の数を扱っているか、疑問に思ったことはありませんか?
私たちが日常で使う数字の表現とは異なり、コンピュータの世界では「補数表現」という特別な方法が用いられています。これは、コンピュータの計算をシンプルにし、効率を高めるための、まさに「魔法の仕組み」と言えます。
この記事では、補数表現について分かりやすく解説しています。特に、コンピュータの数値表現で最も一般的に使われる「2の補数」に焦点を当て、具体例を交えながら深掘りしていきます。
キーワード
- 補数表現
- 2の補数
補数表現とは
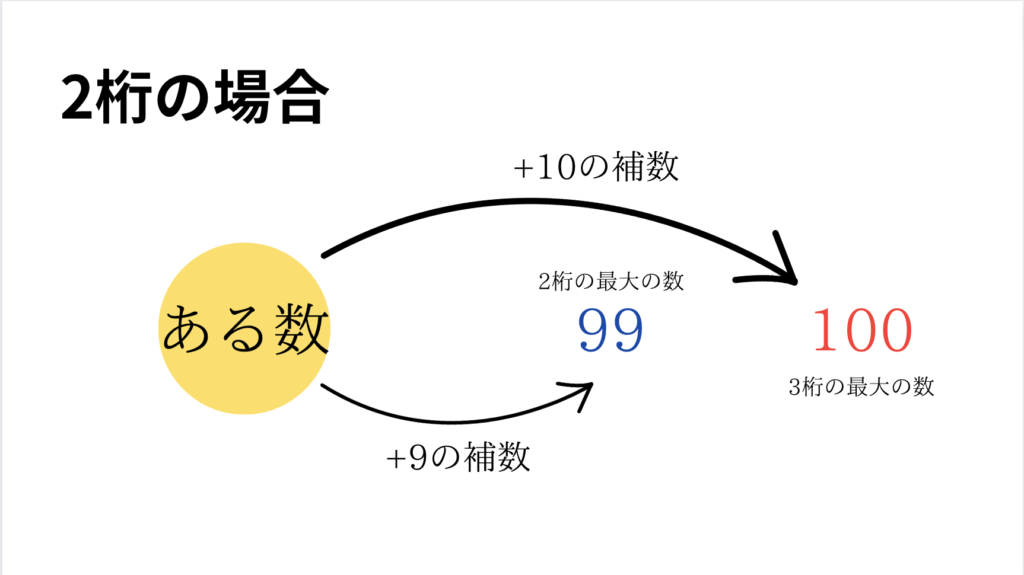
補数とは、「ある数」に足し合わせると、桁が一つ上がるうちの最小の数です。
10進数の「3」であれば「7」が補数に、「125」であれば「875」が補数となります。それぞれ足し合わせると、10と1000となり1桁増えていることが分かります。これを「10の補数」と言います。
また、これとは少し異なる「減基数の補数」というものもあります。減基数の補数とは、「ある数」に足し合わせても、桁が上がらないうちの最大の数です。
先ほどの例で考えていきましょう。10進数の「3」であれば、「9」が1桁の中で最大の数だから「6」が減基数で考えたときの補数になります。同様に、「125」であれば、3桁の中で最大の数「999」にするために874を足し合わせれば良いことから、「874」が減基数で考えたときの補数になります。これを「9の補数」と言います。
一般に、n進数の補数について考えていくときは「nの補数」と「(n – 1)の補数」を考えることができます。nの補数は「ある数」に足し合わせると、桁が一つ上がるうちの最小の数、(n – 1)の補数は「ある数」に足し合わせても、桁が上がらないうちの最大の数です(つまり減基数の補数)。
10進数のときは、「10の補数」と「9の補数」がありましたね。これから考えていくのは2進数の補数です。ということは、「2の補数」と「1の補数」が存在します。
1の補数とは?
2進数の1の補数について考えていきます。(2 – 1)の補数より減基数の補数だから、ある数に足し合わせると桁の繰り上がりが起こらないうちの最大の数が1の補数ということです。

5桁の2進数「10011」をある数とします。5桁の2進数の最大の数は11111となることから、1の補数は1100になります。今回5桁で考えていることから1100を01100とします。\(1100=01100\)です。
さて、ある数と1の補数を比べたときに何か気づくことはありませんか?ある数の各桁の0と1をそれぞれ反転させると1の補数になっています。どうしてそうなるのかピンときていない方は1の補数の定義を思い出してください。桁の繰り上がりが発生しないうちの最大の数は全ての桁が1になることです。ある数に1の補数を足したらこの数になることから、ある数の各桁のうち0になっている桁に1を、1になっている桁には0を足したいため、ある数の各桁を反転させると1の補数になります。0のところを1にしたいからというイメージで大丈夫です。
以上から、各桁を反転させれば1の補数になります。
2の補数とは?
ここでも5桁の2進数「10011」をある数とします。2の補数は、ある数に足し合わせると桁上がりが発生するうちの最小の数です。5桁の繰り上がりなので6桁になる数で最小の数は100000です。よって\(100000-10011=1101\)が2の補数となります。さて、何か気づいたことはありませんか?実は2の補数は1の補数に1を加えた数です。足し合わせた結果が1の補数のときに比べ1大きいことから補数にも1加えます。

以上から、各桁を反転させた後に1加えた数が2の補数になります。
練習問題1
次の2進数について、2の補数をそれぞれ求めなさい。ただし、回答は括弧内の桁数で答えること。
(1)101 (3桁)
(2)01010 (5桁)
(3)101010 (6桁)
回答はこちらから
(1)答え:011
まず各桁(ビットとも言う)をそれぞれ反転させます。101の各ビットを反転させると010。その後、1を加えて011、これが2の補数である。
(2)答え:10110
まず各桁(ビットとも言う)をそれぞれ反転させます。01010の各ビットを反転させると10101。その後、1を加えて10110、これが2の補数である。
(3)答え:010110
まず各桁(ビットとも言う)をそれぞれ反転させます。101010の各ビットを反転させると010101。その後、1を加えて010110、これが2の補数である。
補数表現を用いた引き算
補数表現について理解が深まったと思います。で、結局何に使うの?と疑問が湧いてきた方もいらっしゃるでしょう。

実は、2の補数表現を用いて負の整数を表すとコンピュータにとっては嬉しいのです。コンピュータが計算をするとき、何ビット(桁数のことだと思ってください)でも保存できるわけではありません。どうしても、限界というものがあります。この限界を超えた分のビットは消えてしまいます。そして、ビットが消えるということは、情報が失われるということでもあります。この限界を超えた分のビットが消えてしまう性質によって2の補数が負の整数として振る舞うことができます(詳しい説明は割愛)。
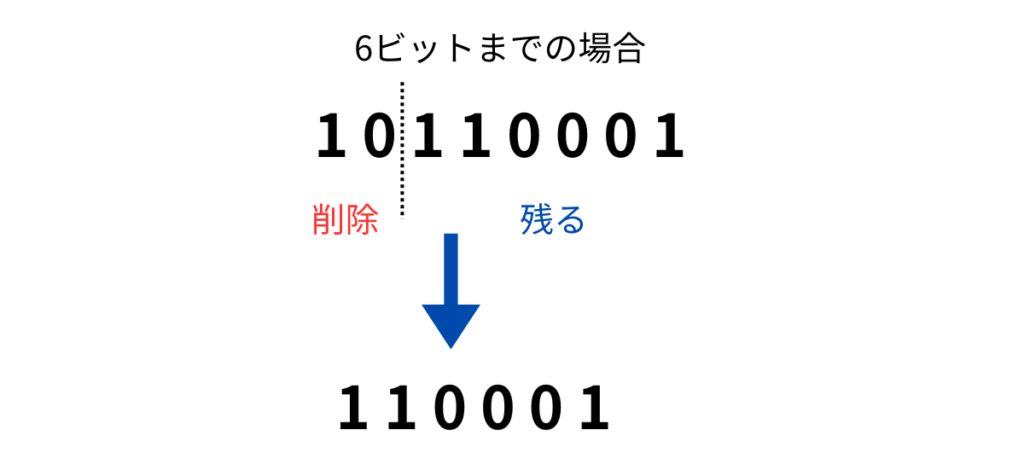
2進数を考える前に、10進数で考えていきましょう。
10進数の引き算、35-13を補数を利用して求めます。-13は負の数なので補数を利用します。13の10の補数は100-13より87です。この87を35に足す、すなわち35-13を35+87で考えます。どういうこと?と思った方もこのまま読んでください。この和35+87=122の最上位の桁を消します。そうすると22が残りました。ここで元の式を見てください。35-13の答えになってますね。負の整数を補数で表すことが出来たと同時に、引き算の問題を足し算にすることができました。
なぜ補数を用いると引き算の問題を足し算の問題へと変えられるか説明します。
-13を87に変えて計算しましたが、87は100-13から求めました。よって35+87 = 35+(100 – 13)が成り立ちます。補数を足し合わせた後、最上位の桁を消したことは100引いたことと同じになります。最上位の数は必ず1になるためです。
これら全ての操作を式にして表すと、
\(35+87-100=35+(100-13)-100=35-13\)
よって補数を足し合わせた後に最上位の数を消すことは、元の式である引き算を考えることと同じであることが分かりました。
今度は2進数の引き算1001-0010を考えます。10進数と同じように考えれば良いです。
まず、負の数-0010を2の補数を使って表します。全てのビットを反転させて1を加えれば良いことから、0010の2の補数は1110です。
この補数を足し合わせると\(1001+1110=10111\)となり、最上位ビットを消して\(0111\)
よって1001-0010の答えが0111と求まりました。実際に直接計算しても答えが一致しました。
補数を使うことで引き算を考えなくてすみました。コンピュータにとっては助かりますね!



コメント