今回は、コンピュータについて学んでいく上で絶対に覚えなくてはいけない2進数について解説します。
10進数と2進数
私たちが日常で扱う数は、10進数と呼ばれるものです。例えば、850円のラーメンに150円の味玉をつけた時の金額は850円+150円=1000円と計算するはずです。これは、各位の数を足して10になったら、次の位に一つ繰り上げるという計算をしています。このように、桁が一つ上がると桁の重み(その桁の値の大きさ)が10倍になります。これを10進数と言います。
では、2進数の場合はどうでしょうか。2進数とは、桁が一つ上がると桁の重みが2倍になる数です。
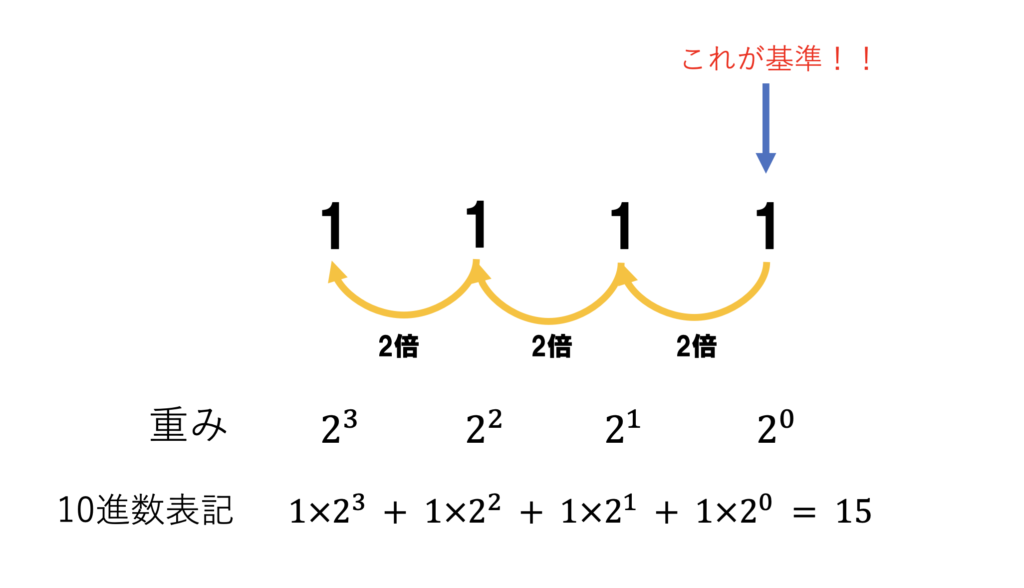
1は10進数でも、2進数でも同じ大きさの数です。この桁のことを一の位と呼んだはずです。ここから、10進数か2進数かで数の大きさが異なっていきます。桁が一つ増えた「10」という数について考えましょう。普段の日常であれば10は”10″です(すごく当たり前のことを言っているだけです)。しかし、2進数の世界は違います。先ほど説明した通り、2進数では桁が一つ上がると桁の重みが2倍になります。そのため、2桁目の重みは1×2=2となります。したがって、10は10進数では1×2+0×1=2となります。
10進数では各位の数を0〜9までの数を用いて表しました。なぜなら、ある位の数がもし10になったのであれば、次の位に1繰り上がり、その位は0になるためです。2進数の場合も同じように考えていきましょう。もし、ある位の数が2になったとき、次の位に1繰り上がり、その位は0になってしまいます。つまり、2進数は0と1で表現される数ということです。
【発展】n進数とは
n進数(ただしnは自然数)とは、桁が一つ上がると、その桁の重みはn倍になる数です。
例として、16進数について考えていきましょう。16進数もこれからIT関連を学んでいく上で重要になります。
16進数で表された「1a」という数を10進数に直してみましょう。16進数ということは一つ桁が上がると、その桁の重みは16倍になるということです。よって2桁目の「1」は10進数に変換すると1×16=16となります。
では1桁目の「a」はどうでしょうか。そもそもaって文字だから数じゃないじゃんと、思うかもしれませんが、10以降の数は文字で表します。対応は以下の通りです。
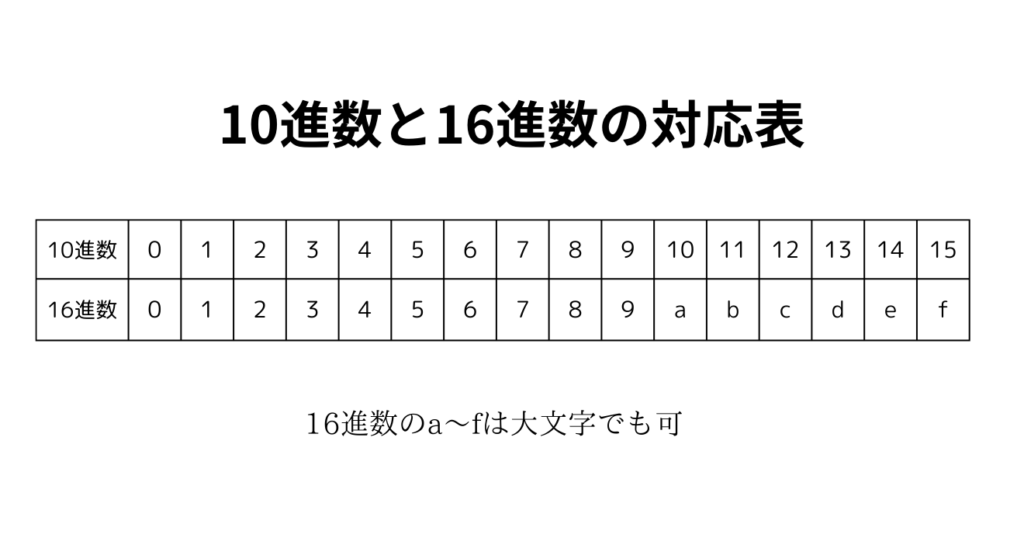
対応表の通り、a〜fを用いて10〜15を表現します。よって「a」は10進数では10となり、「1a」は10進数で表すと1×16+10×1=26となります。今回は英小文字を使いましたが、英大文字でも問題ありません。
3進数、8進数、11進数でも同じように考えていただければ大丈夫です。
確認問題1
次の2進数で表された数を10進数へと変換しなさい。
(1)101
(2)1011
(3)11111
回答はこちら
(1)2進数「101」を10進数へと変換
答え:5
2進数は桁が一つ上がると、重みが2倍になる数でした。よってそれぞれの桁の重みは左から順に[pmath]2^2[/pmath],[pmath]2^1[/pmath],[pmath]2^0[/pmath]となるから、[pmath]1*2^2+0*2^1+1*2^0=5[/pmath]です。
(2)2進数「1011」を10進数へと変換
答え:11
それぞれの桁の重みは左から順に[pmath]2^3, 2^2, 2^1, 2^0[/pmath]となるから、[pmath]1*2^3+0*2^2+1*2^1+1*2^0=11[/pmath]です。
(3)2進数「11111」を10進数へと変換
答え:31
この2進数は100000から1を引いた数になります。2進数100000は[pmath]1*2^5=32[/pmath]より32-1=31が答えです。もちろん、それぞれの重みを考えて足し合わせても答えは一致します。
2進数で表す小数
今までは、自然数について扱いました。では小数の場合はどうでしょうか。
2進数で表された11.01を10進数に変換する場合を考えます。復習ですが、2進数とは一つ桁が増えると、桁の重みが2倍になる数です。ということは、桁が一つ減ると重みは[pmath size=15]1/2[/pmath]倍になるということです。
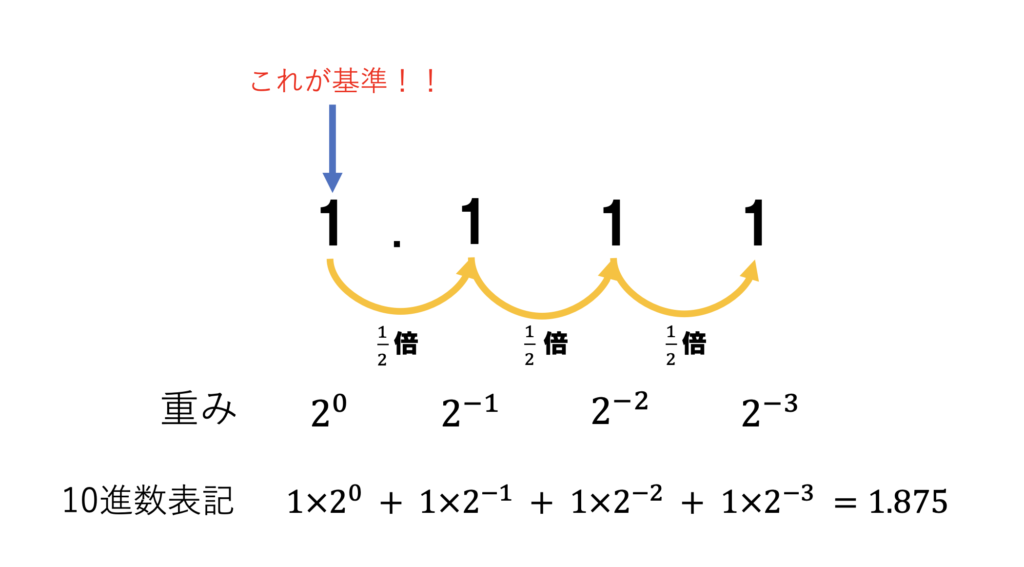
まず整数部分である11を10進数に変換しましょう。1×2+1×1=3となります。
次は小数部分です。重みが1(これが基準)のところから右へ一ついった数の重みは[pmath]1/2[/pmath]となります。そして、さらに右へ一つ移動すると、桁の重みは基準の[pmath](1/2)^2[/pmath]倍になることから、この桁(小数第二位)の重みは[pmath]1/4[/pmath]です。したがって、0.01を10進数に変換すると、[pmath]0*~1/2+1*~1/4=0.25[/pmath]となります。
あとは、整数部分と小数部分を足し合わせるだけです。3+0.25=3.25より2進数11.01を10進数に直すと、3.25となります!
小数がある時は、整数部分と小数部分に分けて考えると良いです。
ちなみに、n進数の場合は一桁下がるごとに、重みは[pmath]1/n[/pmath]になります。それぞれの桁の重みをかけて足し合わせれば、10進数に変換することが可能です。
確認問題2
次の2進数で表された数を10進数に変換しなさい。
(1)10.01
(2)1111.1101
回答はこちら
(1)2進数「10.01」を10進数へ変換する
答え:2.25
それぞれの桁の重みを考えて、[pmath]1*2^1+0*2^0+0*2^-1+1*2^-2=2.25[/pmath]である。
(2)2進数「1111.1101」を10進数へ変換する
答え:15.8125
整数部分は15、小数部分は[pmath]1*2^-1+1*2^-2+0*2^-3+1*2^-4=0.8125[/pmath]であるから、15+0.8125=15.8125である。
2進数同士の足し算と引き算
2進数の足し算と引き算は繰り上がりの数に注意して計算すれば簡単です。普段の計算(10進数の計算)では同じ位の数の和が10になったら、次の位に1を繰り上げて計算しました。2進数の場合では、同じ位の数の和が2になったら、次の位に1を繰り上げます。2進数は桁が一つ上がるごとに、重みが2倍になることからこの計算は自然ですね。
2進数で表された、[pmath]10+11[/pmath]について考えます。一桁目を計算すると、0+1=1となります。次に二桁目を計算すると1+1=10となり、10進数では2となるから、三桁目に1を繰り上げて、二桁目は0となります。3桁目は先ほど繰り上げた1となり、答えは101と分かりました。
また、2進数で考えるのではなく、10進数に一度変換して計算する方法もあります。2進数10は10進数では2、11は3となるから、2+3=5が答えとなり、5を2進数で表すと101となることから、正しいことが分かりました。
練習問題3
次の2進数の式を計算しなさい。ただし、答えは2進数で答えること。
(1)101+11
(2)1001+101
(3)10.01+110.11
回答はこちら
(1)答え:1000
(2)答え:1110
(3)答え:1001



コメント